🚢 Succinct Ships: Optimized bn254 & bls12-381 Precompiles in SP1

TL;DR: Our intern "Bhargav the Great" went wild coding on SP1 for his summer internship and now Fred Ehrsam follows him on X.

• He shipped new precompiles for accelerating bn254 and bls12-381 elliptic curve operations, making SP1 the only production-ready zkVM with these available today.
• These precompiles enable fast proving of the following:
  • verification of groth16 & plonk-kzg proofs within SP1 programs
  • fast bls12-381 EC arithmetic for KZG & blob operations required in Ethereum
  • fast bn254 arithmetic and pairing computation for proving EVM execution (using revm) which gives a massive performance boost to RSP and OP-Succinct.
  • optimized Ethereum ZK Light client with SP1 Helios
• You can start using it today with SP1 v2.0.0 or v3.0.0, reach out if you have any questions!

Background on bn254, bls12-381 & SP1 precompiles

The bn254 and bls12-381 elliptic curves are commonly used elliptic curves in the Ethereum ecosystem. Many protocols use bls12-381 for digital signatures, like Ethereum’s consensus, and various ZKP protocols (like ZCash). The bn254 curve is so popular that it has been enshrined as an Ethereum precompile, and is commonly used for EVM verification of Groth16 and PlonK-KZG proofs.

Examples of bn254 and bls12-381 usage across crypto ecosystems

Due to their prevalence in the Ethereum ecosystem, these elliptic curve operations are also commonly used in SP1 programs. But elliptic curve arithmetic implemented in Rust can be computationally expensive inside SP1, leading to long proof generation times. Thankfully this problem is solved with SP1’s precompiles that provide a major performance boost.

SP1 Precompiles to the Rescue

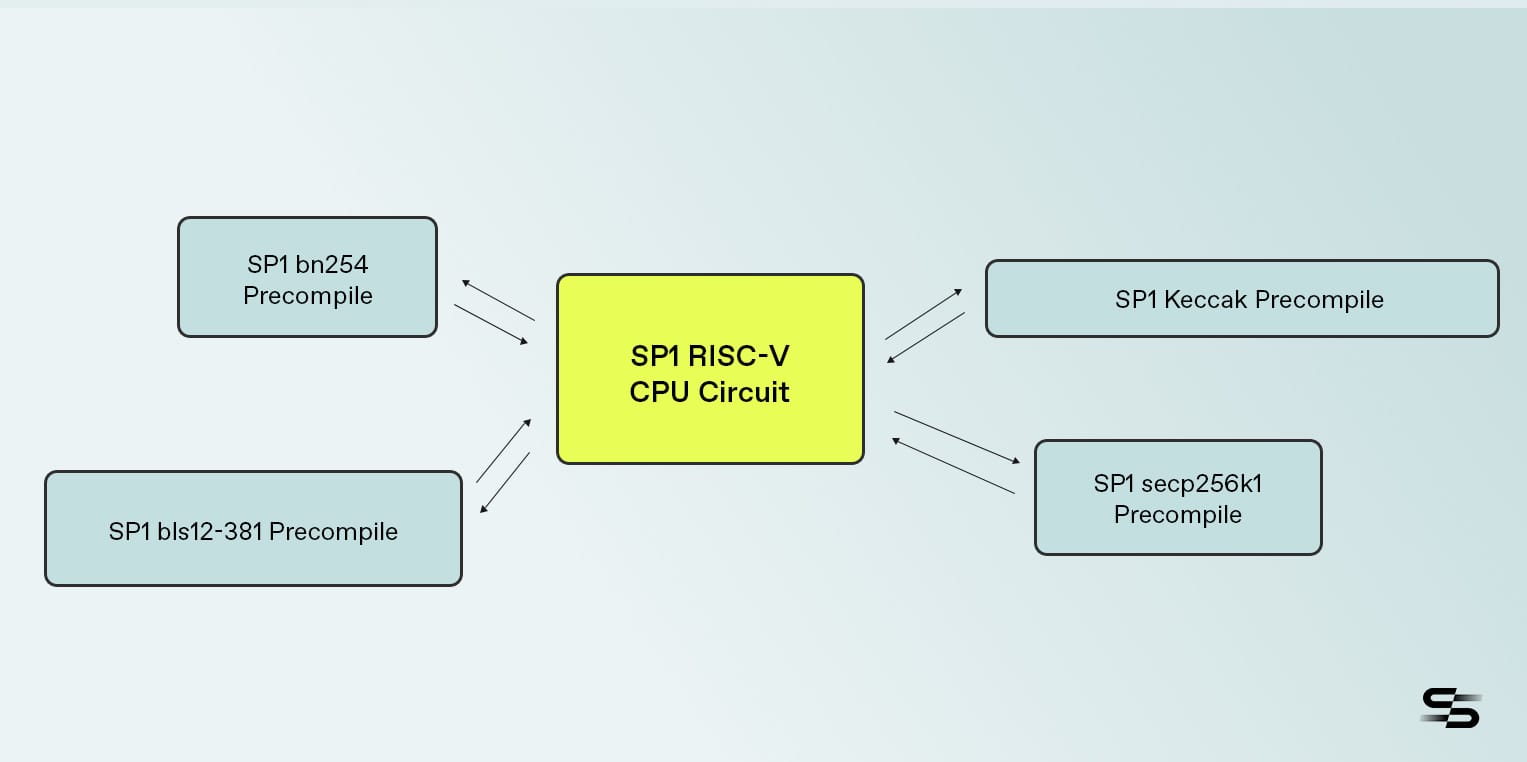
SP1's precompiles are specialized STARKs designed to efficiently compute a common operation, like a hash function or elliptic curve arithmetic. A single precompile invocation is used in place of executing many individual CPU instructions required to carry out a complex task. The specialized precompile circuit is much more efficient at proving the computation vs. many cycles required of our RISC-V CPU table, which incurs overhead from needing to move data to/from registers and memory, and also pays prover overhead from accommodating all possible instructions.

By reducing the number of RISC-V cycles significantly, precompiles typically reduce the computational overhead of proving by several orders of magnitude (check the Appendix for benchmarks).

An Interesting Aside on Elliptic Curve Arithmetic

In traditional CPU execution environments, it is far more efficient to do elliptic curve arithmetic in projective space (P²) because of the high cost of finite field inversions and square roots. However, these otherwise costly operations cost a little more than a field multiplication in the zkVM context--a direct consequence of the general philosophy of "verify don't execute". Thus, we simply need to check that a witnessed value is indeed the correct square root or inverse rather than explicitly finding the value inside of SP1.

Dropping the Cycle Count with Blazing Fast Precompiles

Blazing fast groth16 + plonk-KZG proof verification

Using our bn254 precompiles, we built a sp1-snark-verifier library, for verifying Groth16 or PlonK proofs in SP1, which is useful for generic proof aggregation. SP1 itself also generates Groth16 proofs of PlonK proofs for EVM verification, and you can use this library to use SP1 to recursively verify proofs of itself! 

Using the bn254 precompiles  significantly boosts performance by ~20x for both Groth16 and PlonK proof verification.

Blazing fast kzg-rs blob verification

The KZG polynomial commitment scheme is a cryptographic method used to efficiently prove polynomial evaluations. In Ethereum, KZG commitments are required for EIP-4844, a recent update that enables Ethereum scaling through ephemeral “blobs” data type. Blobs are essential for Layer 2 rollups to function efficiently because it enables them to publish off-chain transaction data while keeping the consensus chain lightweight.

In kzg-rs, we implement a pure Rust crate for KZG blob and batched blob verification for EIP-4844. kzg-rs is valuable for multiple reasons. Firstly, it is a pure Rust implementation of c-kzg-4844 (a popular KZG implementation), which utilizes C bindings, thereby enhancing auditability and portability. Additionally, kzg-rs is optimized to run inside of SP1 and is currently employed for blob verification and KZG point evaluation in OP Succinct, Reth Succinct Processor (RSP) and Taiko's rollup implementation.

Blazing fast Ethereum light client using bls12-381 precompiles

We took Helios, a portable Ethereum light client written in Rust, and combined it with SP1 to create SP1-Helios, a ZK Ethereum light client that is useful for cross-chain interoperability.

With our optimized bls12-381 precompiles for signature verification, verifying 512 signatures from the Ethereum sync committee inside SP1 went from 6 billion cycles to only 50 million.

Blazing fast bn254 pairing in revm

We can use our drop-in replacement for substrate-bn, a fork of the original substrate-bn, to accelerate all bn254 precompiles in Revm. Our substate-bn patch is already incorporated into many of our integrations, including op-succinct and rsp. With 0 lines of code changes to revm, we are able to significantly accelerate all bn254 EVM precompiles, including a 20x speedup in the alt_bn128_pair operation.

Accelerate Your SP1 Program Today

Program too slow? Use SP1, the only zkVM with bn254 and bls12-381 precompiles, and experience the dramatic, order of magnitude speed up yourself. Don’t forget to check out our other long list of precompiles, including keccak256, sha256, secp256k1 and much more. Please get in touch with us here if:

• You’re interested in creating your own precompile or want a specific precompile to accelerate your program–we love collaborating with teams.
• You’re interested in use cases that leverage these precompiles such as kzg verification, RSP, OP-Succinct, SP1-Helios, etc.

Code: Our code is fully open-source with an MIT license: check out SP1 here and feel free to contribute.

Appendix

Precompiles in Action

Below, we show examples of various elliptic curve operations in SP1 by comparing the raw Rust cycle count (number of RISC-V cycles) vs. the cycle count with precompiles.

Precompiles in Action

Below, we show examples of various elliptic curve operations in SP1 by comparing the raw Rust cycle count (number of RISC-V cycles) vs. the cycle count with precompiles.

Base Field (𝐹ₚ) Operations

Quadratic Extension Field (𝐹ₚ2) Operations

𝐹ₚ6 Operations

𝐹ₚ12 Operations

𝐺₁ Projective Curve Operations

𝐺₂ Projective Curve Operations

1 | Also known as bn128 or alt-bn128

2 | Behind the scenes this is a RISC-V ecall (i.e. system call instruction)